Posted on

mdds::multi_type_matrix performance consideration

Share Button

In my previous post, I explained the basic concept of multi_type_vector – one of the two new data structures added to mdds in the 0.6.0 release. In this post, I’d like to explain a bit more about multi_type_matrix – the other new structure added in the aforementioned release. It is also important to note that the addition of multi_type_matrix deprecates mixed_type_matrix, and is subject to deletion in future releases.

Basics

In short, multi_type_matrix is a matrix data structure designed to allow storage of four different element types: numeric value (double), boolean value (bool), empty value, and string value. The string value type can be either std::string, or one provided by the user. Internally, multi_type_matrix is just a wrapper to multi_type_vector, which does most of the hard work. All multi_type_matrix does is to translate logical element positions in 2-dimensional space into one-dimensional positions, and pass them onto the vector. Using multi_type_vector has many advantages over the previous matrix class mixed_type_matrix both in terms of ease of use and performance.

One benefit of using multi_type_vector as its backend storage is that, we will no longer have to differentiate densely-populated and sparsely-populated matrix density types. In mixed_type_matrix, the user would have to manually specify which backend type to use when creating an instance, and once created, it wasn’t possible to switch from one to the other unless you copy it wholesale. In multi_type_matrix, on the other hand, the user no longer has to specify the density type since the new storage is optimized for either density type.

Another benefit is the reduced storage cost and improved latency in memory access especially when accessing a sequence of element values at once. This is inherent in the use of multi_type_vector which I explained in detail in my previous post. I will expand on the storage cost of multi_type_matrix in the next section.

Storage cost

The new multi_type_matrix structure generally provides better storage efficiency in most average cases. I’ll illustrate this by using the two opposite extreme density cases.

First, let’s assume we have a 5-by-5 matrix that’s fully populated with numeric values. The following picture illustrates how the element values of such numeric matrix are stored.

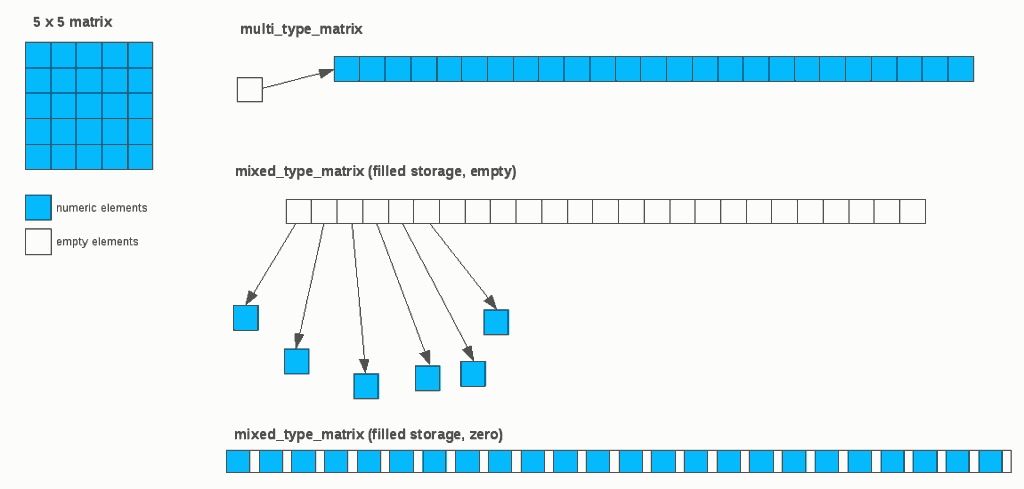
In mixed_type_matrix with its filled-storage backend, the element values are either 1) stored in heap-allocated element objects and their pointers are stored in a separate array (middle right), or 2) stored directly in one-dimensional array (lower right). Those initialized with empty elements employ the first variant, whereas those initialized with zero elements employ the second variant. The rationale behind using these two different storage schemes was the assertion that, in a matrix initialized with empty elements, most elements likely remain empty throughout its life time whereas a matrix initialized with zero elements likely get numeric values assigned to most of the elements for subsequent computations.

Also, each element in mixed_type_matrix stores its type as an enum value. Let’s assume that the size of a pointer is 8 bytes (the world is moving toward 64-bit systems these days), that of a double is 8 bytes, and that of an enum is 4 bytes. The total storage cost of a 5-by-5 matrix will be 8 x 25 + (8 + 4) x 25 = 500 bytes for empty-initialized matrix, and (8 + 4) x 25 = 300 bytes for zero-initialized matrix.

In contrast, multi_type_matrix (upper right) stores the same data using a single array of double’s, whose memory address is stored in a separate block array. This block array also stores the type of each block (int) and its size (size_t). Since we only have one numeric block, it only stores one int value, one size_t value, and one pointer value for the whole block. With that, the total storage cost of a 5-by-5 matrix will be 8 x 25 + 4 + 8 + 8 = 220 bytes. Suffice it to say that it’s less than half the storage cost of empty-initialized mixed_type_matrix, and roughly 26% less than that of zero-initialized mixed_type_matrix.

Now let’s a look at the other end of the density spectrum. Say, we have a very sparsely-populated 5-by-5 matrix, and only the top-left and bottom-right elements are non-empty like the following illustration shows:

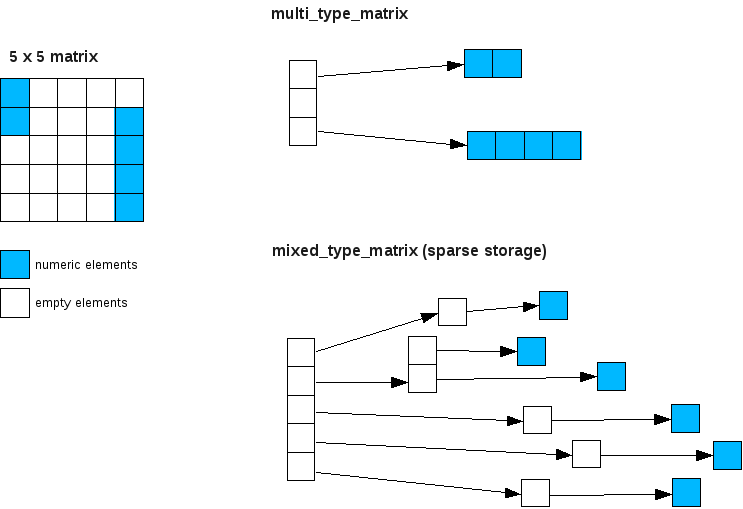
In mixed_type_matrix with its sparse-storage backend (lower right), the element values are stored in heap-allocated element objects which are in turn stored in nested balanced-binary trees. The space requirement of the sparse-storage backend varies depending on how the elements are spread out, but in this particular example, it takes one 5-node tree, one 2-node tree, four single-node tree, and five element instances. Let’s assume that each node in each of these trees stores 3 pointers (pointer to left node, pointer right node and pointer to the value), which makes up 24 bytes of storage per node. Multiplying that by 11 makes 24 x 11 = 264 bytes of storage. With each element instance requiring 12 bytes of storage, the total storage cost comes to 24 x 11 + 12 x 6 = 336 bytes.

In multi_type_matrix (upper right), the primary array stores three element blocks each of which makes up 20 bytes of storage (one pointer, one size_t and one int). Combine that with one 2-element array (16 bytes) and one 4-element array (24 bytes), and the total storage comes to 20 x 3 + 8 * (2 + 4) = 108 bytes. This clearly shows that, even in this extremely sparse density case, multi_type_matrix provides better storage efficiency than mixed_type_matrix.

I hope these two examples are evidence enough that multi_type_matrix provides reasonable efficiency in either densely populated or sparsely populated matrices. The fact that one storage can handle either extreme also gives us more flexibility in that, even when a matrix object starts out sparsely populated then later becomes completely filled, there is no need to manually switch the storage structure as was necessary with mixed_type_matrix.

Run-time performance

Better storage efficiency with multi_type_matrix over mixed_type_matrix is one thing, but what’s equally important is how well it performs run-time. Unfortunately, the actual run-time performance largely depends on how it is used, and while it should provide good overall performance if used in ways that take advantage of its structure, it may perform poorly if used incorrectly.

In this section, I will provide performance comparisons between multi_type_matrix and mixed_type_matrix in several difference scenarios, with the actual source code used to measure their performance. All performance comparisons are done in terms of total elapsed time in seconds required to perform each task. All elapsed times were measured in CPU time, and all benchmark codes were compiled on openSUSE 12.1 64-bit using gcc 4.6.2 with -Os compiler flag.

For the sake of brevity and consistency, the following typedef’s are used throughout the performance test code.

typedef mdds::mixed_type_matrix<std::string, bool>            mixed_mx_type;
typedef mdds::multi_type_matrix<mdds::mtm::std_string_trait>  multi_mx_type;

Instantiation

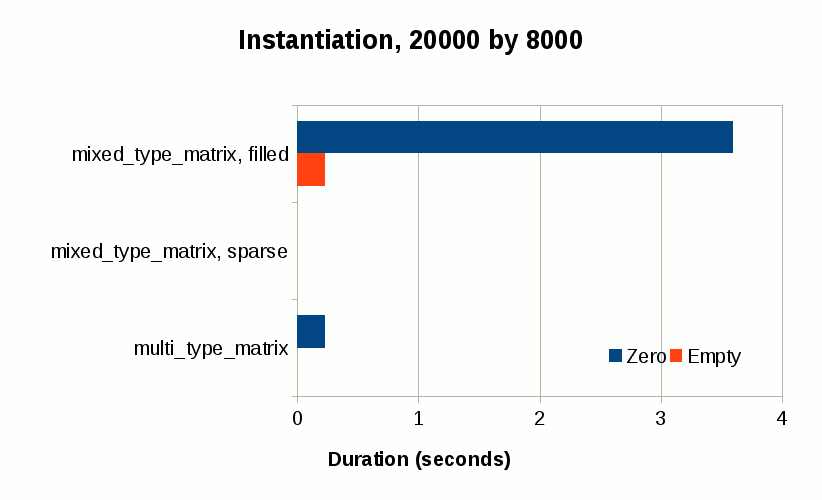
The first scenario is the instantiation of matrix objects. In this test, six matrix object instantiation scenarios are measured. In each scenario, a matrix object of 20000 rows by 8000 columns is instantiated, and the time it takes for the object to get fully instantiated is measured.

The first three scenarios instantiate matrix object with zero element values. The first scenario instantiates mixed_type_matrix with filled storage backend, with all elements initialized to zero.

mixed_mx_type mx(20000, 8000, mdds::matrix_density_filled_zero);

Internally, this allocates a one-dimensional array and fill it with zero element instances.

The second case is just like the first one, the only difference being that it uses sparse storage backend.

mixed_mx_type mx(20000, 8000, mdds::matrix_density_sparse_zero);

With the sparse storage backend, all this does is to allocate just one element instance to use it as zero, and set the internal size value to specified size. No allocation for the storage of any other elements occur at this point. Thus, instantiating a mixed_type_matrix with sparse storage is a fairly cheap, constant-time process.

The third scenario instantiates multi_type_matrix with all elements initialized to zero.

multi_mx_type mx(20000, 8000, 0.0);

This internally allocates one numerical block containing one dimensional array of length 20000 x 8000 = 160 million, and fill it with 0.0 values. This process is very similar to that of the first scenario except that, unlike the first one, the array stores the element values only, without the extra individual element types.

The next three scenarios instantiate matrix object with all empty elements. Other than that, they are identical to the first three.

The first scenario is mixed_type_matrix with filled storage.

mixed_mx_type mx(20000, 8000, mdds::matrix_density_filled_empty);

Unlike the zero element counterpart, this version allocates one empty element instance and one dimensional array that stores all identical pointer values pointing to the empty element instance.

The second one is mixed_type_matrix with sparse storage.

mixed_mx_type mx(20000, 8000, mdds::matrix_density_sparse_empty);

And the third one is multi_type_matrix initialized with all empty elements.

multi_mx_type mx(20000, 8000);

This is also very similar to the initialization with all zero elements, except that it creates one empty element block which doesn’t have memory allocated for data array. As such, this process is cheaper than the zero element counterpart because of the absence of the overhead associated with creating an extra data array.

Here are the results:

The most expensive one turns out to be the zero-initialized mixed_type_matrix, which allocates array with 160 million zero element objects upon construction. What follows is a tie between the empty-initialized mixed_type_matrix and the zero-initialized multi_type_matrix. Both structures allocate array with 160 million primitive values (one with pointer values and one with double values). The sparse mixed_type_matrix ones are very cheap to instantiate since all they need is to set their internal size without additional storage allocation. The empty multi_type_matrix is also cheap for the same reason. The last three types can be instantiated at constant time regardless of the logical size of the matrix.

Assigning values to elements

The next test is assigning numeric values to elements inside matrix. For the remainder of the tests, I will only measure the zero-initialized mixed_type_matrix since the empty-initialized one is not optimized to be filled with a large number of non-empty elements.

We measure six different scenarios in this test. One is for mixed_type_matrix, and the rest are all for multi_type_matrix, as multi_type_matrix supports several different ways to assign values. In contrast, mixed_type_matrix only supports one way to assign values.

The first scenario involves assigning values to elements in mixed_type_matrix. Values are assigned individually inside nested for loops.

size_t row_size = 10000, col_size = 1000;
 
mixed_mx_type mx(row_size, col_size, mdds::matrix_density_filled_zero);
 
double val = 0.0;
for (size_t row = 0; row < row_size; ++row)
{
    for (size_t col = 0; col < col_size; ++col)
    {
        mx.set(row, col, val);
        val += 0.00001; // different value for each element
    }
}

The second scenario is almost identical to the first one, except that it’s multi_type_matrix initialized with empty elements.

size_t row_size = 10000, col_size = 1000;
 
multi_mx_type mx(row_size, col_size);
 
double val = 0.0;
for (size_t row = 0; row < row_size; ++row)
{
    for (size_t col = 0; col < col_size; ++col)
    {
        mx.set(row, col, val);
        val += 0.00001; // different value for each element
    }
}

Because the matrix is initialized with just one empty block with no data array allocated, the very first value assignment allocates the data array just for one element, then all the subsequent assignments keep resizing the data array by one element at a time. Therefore, each value assignment runs the risk of the data array getting reallocated as it internally relies on std::vector’s capacity growth policy which in most STL implementations consists of doubling it on every reallocation.

The third scenario is identical to the previous one. The only difference is that the matrix is initialized with zero elements.

size_t row_size = 10000, col_size = 1000;
 
multi_mx_type mx(row_size, col_size, 0.0);
 
double val = 0.0;
for (size_t row = 0; row < row_size; ++row)
{
    for (size_t col = 0; col < col_size; ++col)
    {
        mx.set(row, col, val);
        val += 0.00001; // different value for each element
    }
}

But this seemingly subtle difference makes a huge difference. Because the matrix is already initialized with a data array to the full matrix size, none of the subsequent assignments reallocate the array. This cuts the repetitive reallocation overhead significantly.

The next case involves multi_type_matrix initialized with empty elements. The values are first stored into an extra array first, then the whole array gets assigned to the matrix in one call.

size_t row_size = 10000, col_size = 1000;
 
multi_mx_type mx(row_size, col_size);
 
// Prepare a value array first.
std::vector<double> vals;
vals.reserve(row_size*col_size);
double val = 0.0;
for (size_t row = 0; row < row_size; ++row)
{
    for (size_t col = 0; col < col_size; ++col)
    {
        vals.push_back(val);
        val += 0.00001;
    }
}
 
// Assign the whole element values in one step.
mx.set(0, 0, vals.begin(), vals.end());

Operation like this is something that mixed_type_matrix doesn’t support. What the set() method on the last line does is to assign the values to all elements in the matrix in one single call; it starts from the top-left (0,0) element position and keeps wrapping values into the subsequent columns until it reaches the last element in the last column.

Generally speaking, with multi_type_matrix, assigning a large number of values in this fashion is significantly faster than assigning them individually, and even with the overhead of the initial data array creation, it is normally faster than individual value assignments. In this test, we measure the time it takes to set values with and without the initial data array creation.

The last scenario is identical to the previous one, but the only difference is the initial element values being zero instead of being empty.

size_t row_size = 10000, col_size = 1000;
 
multi_mx_type mx(row_size, col_size, 0.0);
 
// Prepare a value array first.
std::vector<double> vals;
vals.reserve(row_size*col_size);
double val = 0.0;
for (size_t row = 0; row < row_size; ++row)
{
    for (size_t col = 0; col < col_size; ++col)
    {
        vals.push_back(val);
        val += 0.00001;
    }
}
 
// Assign the whole element values in one step.
mx.set(0, 0, vals.begin(), vals.end());

The only significant thing this code does differently from the last one is that it assigns values to an existing numeric data array whereas the code in the previous scenario allocates a new array before assigning values. In practice, this difference should not make any significant difference performance-wise.

Now, let’s a take a look at the results.

The top orange bar is the only result from mixed_type_matrix, and the rest of the blue bars are from multi_type_matrix, using different assignment techniques.

The top three bars are the results from the individual value assignments inside loop (hence the label “loop”). The first thing that jumps out of this chart is that individually assigning values to empty-initialized multi_type_matrix is prohibitively expensive, thus such feat should be done with extra caution (if you really have to do it). When the matrix is initialized with zero elements, however, it does perform reasonably though it’s still slightly slower than the mixed_type_matrix case.

The bottom four bars are the results from the array assignments to multi_type_matrix, one initialized with empty elements and one initialized with zero elements, and one is with the initial data array creation and one without. The difference between the two initialization cases is very minor and well within the margin of being barely noticeable in real life.

Performance of an array assignment is roughly on par with that of mixed_type_matrix’s if you include the cost of the extra array creation. But if you take away that overhead, that is, if the data array is already present and doesn’t need to be created prior to the assignment, the array assignment becomes nearly 3 times faster than mixed_type_matrix’s individual value assignment.

Adding all numeric elements

The next benchmark test consists of fetching all numerical values from a matrix and adding them all together. This requires accessing the stored elements inside matrix after it has been fully populated.

With mixed_type_matrix, the following two ways of accessing element values are tested: 1) access via individual get_numeric() calls, and 2) access via const_iterator. With multi_type_matrix, the tested access methods are: 1) access via individual get_numeric() calls, and 2) access via walk() method which walks all element blocks sequentially and call back a caller-provided function object on each element block pass.

In each of the above testing scenarios, two different element distribution types are tested: one that consists of all numeric elements (homogeneous matrix), and one that consists of a mixture of numeric and empty elements (heterogeneous matrix). In the tests with heterogeneous matrices, one out of every three columns is set empty while the remainder of the columns are filled with numeric elements. The size of a matrix object is fixed to 10000 rows by 1000 columns in each tested scenario.

The first case involves populating a mixed_type_matrix instance with all numeric elements (homogenous matrix), then read all values to calculate their sum.

size_t row_size = 10000, col_size = 1000;
 
mixed_mx_type mx(row_size, col_size, mdds::matrix_density_filled_zero);
 
// Populate the matrix with all numeric values.
double val = 0.0;
for (size_t row = 0; row < row_size; ++row)
{
    for (size_t col = 0; col < col_size; ++col)
    {
        mx.set(row, col, val);
        val += 0.00001;
    }
}
 
// Sum all numeric values.
double sum = 0.0;
for (size_t row = 0; row < row_size; ++row)
    for (size_t col = 0; col < col_size; ++col)
        sum += mx.get_numeric(row, col);

The test only measures the second nested for loops where the values are read and added. The first block where the matrix is populated is excluded from the measurement.

In the heterogeneous matrix variant, only the first block is different:

// Populate the matrix with numeric and empty values.
double val = 0.0;
for (size_t row = 0; row < row_size; ++row)
{
    for (size_t col = 0; col < col_size; ++col)
    {
        if ((col % 3) == 0)
        {
            mx.set_empty(row, col);
        }
        else
        {
            mx.set(row, col, val);
            val += 0.00001;
        }
    }
}

while the second block remains intact. Note that the get_numeric() method returns 0.0 when the element type is empty (this is true with both mixed_type_matrix and multi_type_matrix), so calling this method on empty elements has no effect on the total sum of all numeric values.

When measuring the performance of element access via iterator, the second block is replaced with the following code:

// Sum all numeric values via iterator.
double sum = 0.0;
mixed_mx_type::const_iterator it = mx.begin(), it_end = mx.end();
for (; it != it_end; ++it)
{
    if (it->m_type == mdds::element_numeric)
        sum += it->m_numeric;
}

Four separate tests are performed with multi_type_matrix. The first variant consists of a homogeneous matrix with all numeric values, where the element values are read and added via manual loop.

size_t row_size = 10000, col_size = 1000;
 
multi_mx_type mx(row_size, col_size, 0.0);
 
// Populate the matrix with all numeric values.
double val = 0.0;
for (size_t row = 0; row < row_size; ++row)
{
    for (size_t col = 0; col < col_size; ++col)
    {
        mx.set(row, col, val);
        val += 0.00001;
    }
}
 
// Sum all numeric values.
double sum = 0.0;
for (size_t row = 0; row < row_size; ++row)
    for (size_t col = 0; col < col_size; ++col)
        sum += mx.get_numeric(row, col);

This code is identical to the very first scenario with mixed_type_matrix, the only difference being that it uses multi_type_matrix initialized with zero elements.

In the heterogeneous matrix variant, the first block is replaced with the following:

multi_mx_type mx(row_size, col_size); // initialize with empty elements.
double val = 0.0;
vector<double> vals;
vals.reserve(row_size);
for (size_t col = 0; col < col_size; ++col)
{
    if ((col % 3) == 0)
        // Leave this column empty.
        continue;
 
    vals.clear();
    for (size_t row = 0; row < row_size; ++row)
    {
        vals.push_back(val);
        val += 0.00001;
    }
 
    mx.set(0, col, vals.begin(), vals.end());
}

which essentially fills the matrix with numeric values except for every 3rd column being left empty. It’s important to note that, because heterogeneous multi_type_matrix instance consists of multiple element blocks, making every 3rd column empty creates roughly over 300 element blocks with matrix that consists of 1000 columns. This severely affects the performance of element block lookup especially for elements that are not positioned in the first few blocks.

The walk() method was added to multi_type_matrix precisely to alleviate this sort of poor lookup performance in such heavily partitioned matrices. This allows the caller to walk through all element blocks sequentially, thereby removing the need to restart the search in every element access. The last tested scenario measures the performance of this walk() method by replacing the second block with:

sum_all_values func;
mx.walk(func);

where the sum_all_values function object is defined as:

class sum_all_values : public std::unary_function<multi_mx_type::element_block_node_type, void>
{
    double m_sum;
public:
    sum_all_values() : m_sum(0.0) {}
 
    void operator() (const multi_mx_type::element_block_node_type& blk)
    {
        if (!blk.data)
            // Skip the empty blocks.
            return;
 
        if (mdds::mtv::get_block_type(*blk.data) != mdds::mtv::element_type_numeric)
            // Block is not of numeric type.  Skip it.
            return;
 
        using mdds::mtv::numeric_element_block;
        // Access individual elements in this block, and add them up.
        numeric_element_block::const_iterator it = numeric_element_block::begin(*blk.data);
        numeric_element_block::const_iterator it_end = numeric_element_block::end(*blk.data);
        for (; it != it_end; ++it)
            m_sum += *it;
    }
 
    double get() const { return m_sum; }
};

Without further ado, here are the results:

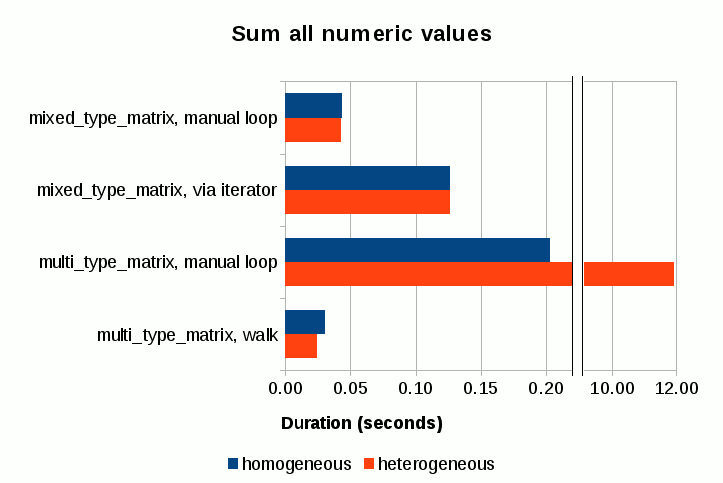
It is somewhat surprising that mixed_type_matrix shows poorer performance with iterator access as opposed to access via get_numeric(). There is no noticeable difference between the homogeneous and heterogeneous matrix scenarios with mixed_type_matrix, which makes sense given how mixed_type_matrix stores its element values.

On the multi_type_matrix front, element access via individual get_numeric() calls turns out to be very slow, which is expected. This poor performance is highly visible especially with heterogeneous matrix consisting of over 300 element blocks. Access via walk() method, on the other hand, shows much better performance, and is in fact the fastest amongst all tested scenarios. Access via walk() is faster with the heterogeneous matrix which is likely attributed to the fact that the empty element blocks are skipped which reduces the total number of element values to read.

Counting all numeric elements

In this test, we measure the time it takes to count the total number of numeric elements stored in a matrix. As with the previous test, we use both homogeneous and heterogeneous 10000 by 1000 matrix objects initialized in the same exact manner. In this test, however, we don’t measure the individual element access performance of multi_type_matrix since we all know by now that doing so would result in a very poor performance.

With mixed_type_matrix, we measure counting both via individual element access and via iterators. I will not show the code to initialize the element values here since that remains unchanged from the previous test. The code that does the counting is as follows:

// Count all numeric elements.
long count = 0;
for (size_t row = 0; row < row_size; ++row)
{
    for (size_t col = 0; col < col_size; ++col)
    {
        if (mx.get_type(row, col) == mdds::element_numeric)
            ++count;
    }
}

It is pretty straightforward and hopefully needs no explanation. Likewise, the code that does the counting via iterator is as follows:

// Count all numeric elements via iterator.
long count = 0;
mixed_mx_type::const_iterator it = mx.begin(), it_end = mx.end();
for (; it != it_end; ++it)
{
    if (it->m_type == mdds::element_numeric)
        ++count;
}

Again a pretty straightforward code.

Now, testing this scenario with multi_type_matrix is interesting because it can take advantage of multi_type_matrix’s block-based element value storage. Because the elements are partitioned into multiple blocks, and each block stores its size separately from the data array, we can simply tally the sizes of all numeric element blocks to calculate its total number without even counting the actual individual elements stored in the blocks. And this algorithm scales with the number of element blocks, which is far fewer than the number of elements in most average use cases.

With that in mind, the code to count numeric elements becomes:

count_all_values func;
mx.walk(func);

where the count_all_values function object is defined as:

class count_all_values : public std::unary_function<multi_mx_type::element_block_node_type, void>
{
    long m_count;
public:
    count_all_values() : m_count(0) {}
    void operator() (const multi_mx_type::element_block_node_type& blk)
    {
        if (!blk.data)
            // Empty block.
            return;
 
        if (mdds::mtv::get_block_type(*blk.data) != mdds::mtv::element_type_numeric)
            // Block is not numeric.
            return;
 
        m_count += blk.size; // Just use the separate block size.
    }
 
    long get() const { return m_count; }
};

With mixed_type_matrix, you are forced to parse all elements in order to count elements of a certain type regardless of which type of elements to count. This algorithm scales with the number of elements, much worse proposition than scaling with the number of element blocks.

Now that the code has been presented, let move on to the results:

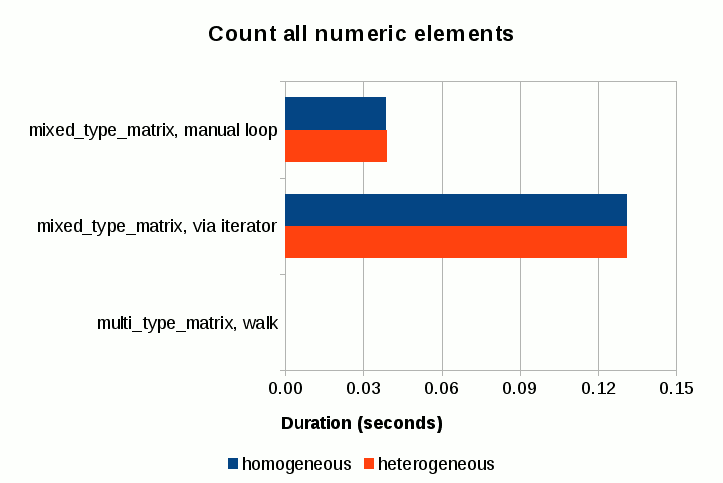
The performance of mixed_type_matrix, both manual loop and via iterator cases, is comparable to that of the previous test. What’s remarkable is the performance of multi_type_matrix via its walk() method; the numbers are so small that they don’t even register in the chart! As I mentions previously, the storage structure of multi_type_matrix replaces the problem of counting elements into a new problem of counting element blocks, thereby significantly reducing the scale factor with respect to the number of elements in most average use cases.

Initializing matrix with identical values

Here is another scenario where you can take advantage of multi_type_matrix over mixed_type_matrix. Say, you want to instantiate a new matrix and assign 12.3 to all of its elements. With mixed_type_matrix, the only way you can achieve that is to assign that value to each element in a loop after it’s been constructed. So you would write code like this:

size_t row_size = 10000, col_size = 2000;
mixed_mx_type mx(row_size, col_size, mdds::matrix_density_filled_zero);
 
for (size_t row = 0; row < row_size; ++row)
    for (size_t col = 0; col < col_size; ++col)
        mx.set(row, col, 12.3);

With multi_type_matrix, you can achieve the same result by simply passing an initial value to the constructor, and that value gets assigned to all its elements upon construction. So, instead of assigning it to every element individually, you can simply write:

multi_mx_type(row_size, col_size, 12.3);

Just for the sake of comparison, I’ll add two more cases for multi_type_matrix. The first one involves instantiation with a numeric block of zero’s, and individually assigning value to the elements afterward, like so:

multi_mx_type mx(row_size, col_size, 0.0);
 
for (size_t row = 0; row < row_size; ++row)
    for (size_t col = 0; col < col_size; ++col)
        mx.set(row, col, 12.3);

which is algorithmically similar to the mixed_type_matrix case.

Now, the second one involves instantiation with a numeric block of zero’s, create an array with the same element count initialized with a desired initial value, then assign that to the matrix in one go.

multi_mx_type mx(row_size, col_size);
 
vector<double> vals(row_size*col_size, 12.3);
mx.set(0, 0, vals.begin(), vals.end());

The results are:

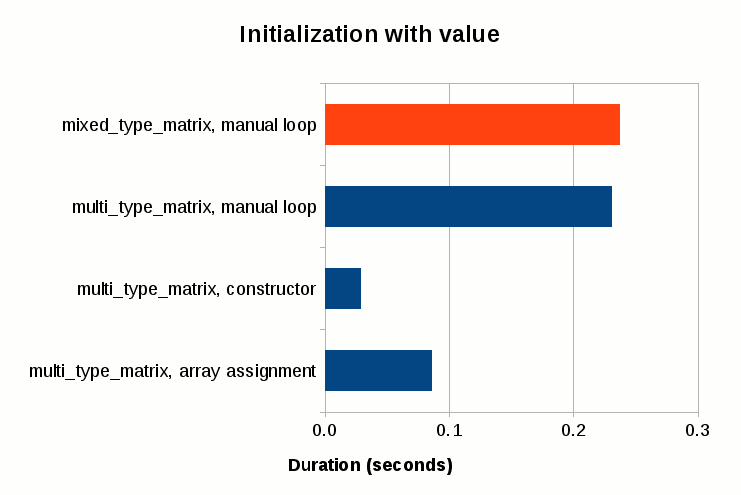
The performance of assigning initial value to individual elements is comparable between mixed_type_matrix and multi_type_matrix, though it is also the slowest of all. Creating an array of initial values and assigning it to the matrix takes less than half the time of individual assignment even with the overhead of creating the extra array upfront. Passing an initial value to the constructor is the fastest of all; it only takes roughly 1/8th of the time required for the individual assignment, and 1/3rd of the array assignment.

Conclusion

I hope I have presented enough evidence to convince you that multi_type_matrix offers overall better performance than mixed_type_matrix in a wide variety of use cases. Its structure is much simpler than that of mixed_type_matrix in that, it only uses one element storage backend as opposed to three in mixed_type_matrix. This greatly improves not only the cost of maintenance but also the predictability of the container behavior from the user’s point of view. That fact that you don’t have to clone matrix just to transfer it into another storage backend should make it a lot simpler to use this new matrix container.

Having said this, you should also be aware of the fact that, in order to take full advantage of multi_type_matrix to achieve good run-time performance, you need to

  • try to limit single value assignments and prefer using value array assignment,
  • construct matrix with proper initial value which also determines the type of initial element block, which in turn affects the performance of subsequent value assignments, and
  • use the walk() method when iterating through all elements in the matrix.

That’s all, ladies and gentlemen.

Posted on

Ixion – threaded formula calculation library

Share Button

I spent my entire last week on my personal project, by taking advantage of Novell’s HackWeek. Officially, HackWeek took place two weeks ago, but because I had to travel that week I postponed mine till the following week.

Ixion is the project I worked on as part of my HackWeek. This project is an experimental effort to develop a stand-alone library that supports parallel computation of formula expressions using threads. I’d been working on this on and off in my spare time, but when the opportunity came along to spend one week of my paid time on any project of my choice (personal or otherwise), I didn’t hesitate to pick Ixion.

Overview

So, what’s Ixion? Ixion aims to provide a library for calculating the results of formula expressions stored in multiple named targets, or “cells”. The cells can be referenced from each other, and the library takes care of resolving their dependencies automatically upon calculation. The caller can run the calculation routine either in a single-threaded mode, or a multi-threaded mode. The library also supports re-calculation where the contents of one or more cells have been modified since the last calculation, and a partial calculation of only the affected cells gets performed. It is written entirely in C++, and makes extensive use of the boost library to achieve portability across different platforms. It has currently been tested to build on Linux and Windows.

The goal is to eventually bring this library up to the level where it can serve as a full-featured calculation engine for spreadsheet applications. But right now, this project remains as an experimental, proof-of-concept project to help me understand what is required to build a threaded calculation engine capable of performing all sorts of tasks required in a typical spreadsheet app.

I consider this project a library project; however, building this project only creates a single stand-alone console application at the moment. I plan to separate it into a shared library and a front-end executable in the future, to allow external apps to dynamically link to it.

How it works

Building this project creates an executable called ixion-parser. Running it with a -h option displays the following help content:

Usage: ixion-parser [options] FILE1 FILE2 ...
 
The FILE must contain the definitions of cells according to the cell definition rule.
 
Allowed options:
  -h [ --help ]         print this help.
  -t [ --thread ] arg   specify the number of threads to use for calculation.  
                        Note that the number specified by this option 
                        corresponds with the number of calculation threads i.e.
                        those child threads that perform cell interpretations. 
                        The main thread does not perform any calculations; 
                        instead, it creates a new child thread to manage the 
                        calculation threads, the number of which is specified 
                        by the arg.  Therefore, the total number of threads 
                        used by this program will be arg + 2.

The parser expects one or more cell definition files as arguments. A cell definition file may look like this:

%mode init
A1=1
A2=A1+10
A3=A2+A1*30
A4=(10+20)*A2
A5=A1-A2+A3*A4
A6=A1+A3
A7=A7
A8=10/0
A9=A8
%calc
%mode result
A1=1
A2=11
A3=41
A4=330
A5=13520
A6=42
A7=#REF!
A8=#DIV/0!
A9=#DIV/0!
%check
%mode edit
A6=A1+A2
%recalc
%mode result
A1=1
A2=11
A3=41
A4=330
A5=13520
A6=12
A7=#REF!
A8=#DIV/0!
A9=#DIV/0!
%check
%mode edit
A1=10
%recalc

I hope the format of the cell definition rule is straightforward. The definitions are read from top down. I used the so-called A1 notation to name target cells, but it doesn’t have to be that way. You can use any naming scheme to name target cells as long as the lexer recognizes them as names. Also, the format supports a command construct; a line beginning with a ‘%’ is considered a command. Several commands are currently available. For instance the mode command lets you switch input modes. The parser currently supports three input modes:

  • init – initialize cells with specified contents.
  • result – pick up expected results for cells, for verification.
  • edit – modify cell contents.

In addition to the mode command, the following commands are also supported:

  • calc – perform full calculation, by resetting the cached results of all involved cells.
  • recalc – perform partial re-calculation of modified cells and cells that reference modified cells, either directly or indirectly.
  • check – verify the calculation results.

Given all this, let’s see what happens when you run the parser with the above cell definition file.

./ixion-parser -t 4 test/01-simple-arithmetic.txt 
Using 4 threads
Number of CPUS: 4
---------------------------------------------------------
parsing test/01-simple-arithmetic.txt
---------------------------------------------------------
A1: 1
A1: result = 1
---------------------------------------------------------
A2: A1+10
A2: result = 11
---------------------------------------------------------
A3: A2+A1*30
A3: result = 41
---------------------------------------------------------
A4: (10+20)*A2
A4: result = 330
---------------------------------------------------------
A5: A1-A2+A3*A4
A5: result = 13520
---------------------------------------------------------
A8: 10/0
result = #DIV/0!
---------------------------------------------------------
A6: A1+A3
A6: result = 42
---------------------------------------------------------
A9: 
result = #DIV/0!
---------------------------------------------------------
A7: result = #REF!
---------------------------------------------------------
checking results
---------------------------------------------------------
A2 : 11
A8 : #DIV/0!
A3 : 41
A9 : #DIV/0!
A4 : 330
A5 : 13520
A6 : 42
A7 : #REF!
A1 : 1
---------------------------------------------------------
recalculating
---------------------------------------------------------
A6: A1+A2
A6: result = 12
---------------------------------------------------------
checking results
---------------------------------------------------------
A2 : 11
A8 : #DIV/0!
A3 : 41
A9 : #DIV/0!
A4 : 330
A5 : 13520
A6 : 12
A7 : #REF!
A1 : 1
---------------------------------------------------------
recalculating
---------------------------------------------------------
A1: 10
A1: result = 10
---------------------------------------------------------
A2: A1+10
A2: result = 20
---------------------------------------------------------
A3: A2+A1*30
A3: result = 320
---------------------------------------------------------
A4: (10+20)*A2
A4: result = 600
---------------------------------------------------------
A5: A1-A2+A3*A4
A5: result = 191990
---------------------------------------------------------
A6: A1+A2
A6: result = 30
---------------------------------------------------------
(duration: 0.00113601 sec)
---------------------------------------------------------

Notice that at the beginning of the output, it displays the number of threads being used, and the number of “CPU”s it detected. Here, the “CPU” may refer to the number of physical CPUs, the number of cores, or the number of hyper-threading units. I’m well aware that I need to use a different term for this other than “CPU”, but anyways… The number of child threads to use to perform calculation can be specified at run-time via -t option. When running without the -t option, the parser will run in a single-threaded mode. Now, let me go over what the above output means.

The first calculation performed is a full calculation. Since no cells have been calculated yet, we need to calculate results for all defined cells. This is followed by a verification of the initial calculation. After this, we modify cell A6, and perform partial re-calculation. Since no other cells depend on the result of cell A6, the re-calc only calculates A6.

Now, the third calculation is also a partial re-calculation following the modification of cell A1. This time, because several other cells do depend on the result of A1, those cells also need to be re-calculated. The end result is that cells A1, A2, A3, A4, A5 and A6 all get re-calculated.

Under the hood

Cell dependency resolution

cell-dependency-graph
There are several technical aspects of the implementation of this library I’d like to cover. The first is cell dependency resolution. I use a well-known algorithm called topological sort to sort cells in order of dependency so that cells can be calculated one by one without being blocked by the calculation of precedent cells. Topological sort is typically used to manage scheduling of tasks that are inter-dependent with each other, and it was a perfect one to use to resolve cell dependencies. This algorithm is a by-product of depth first search of directed acyclic graph (DAG), and is well-documented. A quick google search should give you tons of pseudo code examples of this algorithm. This algorithm work well both for full calculation and partial re-calculation routines.

Managing threaded calculation

The heart of this project is to implement parallel evaluation of formula expressions, which has been my number 1 goal from the get-go. This is also the reason why I put my focus on designing the threaded calculation engine as my initial goal before I start putting my focus into other areas. Programming with threads was also very new to me, so I took extra care to ensure that I understand what I’m doing, and I’m designing it correctly. Also, designing a framework that uses multiple threads can easily get out-of-hand and out-of-control when it’s overdone. So, I made an extra effort to limit the area where multiple threads are used while keeping the rest of the code single-threaded, in order to keep the code simple and maintainable.

As I soon realized, even knowing the basics of programming with threads, you are not immune to falling into many pitfalls that may arise during the actual designing and debugging of concurrent code. You have to go extra miles ensuring that access to thread-global data are synchronized, and that one thread waits for another thread in case threads must be executed in certain order. These things may sound like common sense and probably are in every thread programming text book, but in reality they are very easy to overlook, especially to those who have not had substantial exposure to concurrency before. Parallelism seemed that un-orthodox to conventional minds like myself. Having said all that, once you go through enough pain dealing with concurrency, it does become less painful after a while. Your mind can simply adjust to “thinking in parallel”.

Back to the topic. I’ve picked the following pattern to manage threaded calculation.

thread-design

First, the main thread creates a new thread whose job is to manage cell queues, that is, receiving queues from the main thread and assigning them to idle threads to perform calculation. It is also responsible for keeping track of which threads are idle and ready to take on a cell assignment. Let’s call this thread a queue manager thread. When the queue manager thread is created, it spawns a specified number of child threads, and waits until they are all ready. These child threads are the ones that perform cell calculation, and we call them calc threads.

Each calc thread registers itself as an idle thread upon creation, then sleeps until the queue manager thread assigns it a cell to calculate and signals it to wake up. Once awake, it calculates the cell, registers itself as an idle thread once again and goes back to sleep. This cycle continues until the queue manager thread sends a termination request to it, after which it breaks out of the cycle and reaches the end of its execution path to terminate.

The role of the queue manager thread is to receive cell calculation requests from the main thread and pass them on to idle calc threads. It keeps doing it until it receives a termination request from the main thread. Once receiving the termination request from the main thread, it sends all the remaining cells in queue to the calc threads to finish up, then sends termination requests to the calc threads and wait until all of them terminate.

Thanks to the cells being sorted in topological order, the process of putting a cell in queue and having a calc thread perform calculation is entirely asynchronous. The only exception is that when referencing another cell during calculation, the result of that referenced cell may not be available at the time of the value query due to concurrency. In such cases, the calculating thread needs to block its execution until the result of the referenced cell becomes available. When running in a single-threaded mode, on the other hand, the result of a referenced cell is guaranteed to be available as long as cells are calculated in topological order and contain no circular references.

What I accomplished during HackWeek

During HackWeek, I was able to accomplish quite a few things. Before the HackWeek, the threaded calculation framework was not even there; the parser was only able to reliably perform calculation in a single-threaded mode. I had some test code to design the threaded queue management framework, but that code had yet to be integrated into the main formula interpreter code. A lot of work was still needed, but thanks to having an entire week devoted for this, I was able to

  • port the test threaded queue manager framework code into the formula interpreter code,
  • adopt the circular dependency detection code for the new threaded calculation framework,
  • test the new framework to squeeze lots of kinks out,
  • put some performance optimization in the cell definition parser and the formula lexer code,
  • implement result verification framework, and
  • implement partial re-calculation.

Had I had to do all this in my spare time alone, it would have easily taken months. So, I’m very thankful for the event, and I look forward to having another opportunity like this in hopefully not-so-distant future.

What lies ahead

So, what lies ahead for Ixion? You may ask. There are quite a few things to get done. Let me start first by saying that, this library is far from providing all the features that a typical spreadsheet application needs. So, there are still lots of work needed to make it even usable. Moreover, I’m not even sure whether this library will become usable enough for real-world spreadsheet use, or it will simply end up being just another interesting proof-of-concept. My hope is of course to see this library evolve into maturity, but at the same time I’m also aware that it would be hard to advance this project with only my scarce spare time to spend in.

With that said, here are some outstanding issues that I plan on addressing as time permits.

  • Add support for literal strings, and support textural formula results in addition to numerical results.
  • Add support for empty cells. Empty cells are those cells that are not defined in the model definition file but can still be referenced. Currently, referencing a cell that is not defined causes a reference error.
  • Add support for cell ranges. This implies that I need to make cell instances addressable by 3-dimensional coordinates rather than by pointer values.
  • Split the code into two parts: a shared library and an executable.
  • Use autoconf to make the build process configurable.
  • Make the expression parser feature-complete.
  • Implement more functions. Currently only MAX and MIN are implemented.
  • Support for localized numbers.
  • Lots and lots more.

Conclusion

This concludes my HackWeek report. Thank you very much, ladies and gentlemen.

Posted on

Increasing Calc’s row limit to 1 million

Share Button

Introduction

With the child work space (CWS) koheirowlimitperf being marked ready for QA, I believe this is a good time to talk about the change that the CWS will bring once it gets integrated.

The role of this CWS is to upstream various pieces of performance optimization from Go-OO, that arose from the increase of the row limit from 65536 (64 thousand rows) to 1048576 (1 million rows). However, the upstream build will not see the increase of the row limit itself yet, as the upstream developers still consider that move premature due to two outstanding issues that are show stoppers for them. I’ll talk more about those issues later.

What this CWS does change is the storage of row attributes to 1) improve performance of querying the attributes, and to 2) make extra information available that can be used to make the algorithm of various bits of operations more efficient. The CWS also makes several other changes in order to improve performance in general, though not related to the change in the row attribute storage.

Limitation of the old attribute storage

Before I talk about how the row attributes are stored in the new storage, I’d like to talk about the limitation of the old attribute storage, and why it was not adequate when the row limit was raised to 1 million rows. Also, in this article, I’ll only talk about row attribute storage, but the same argument also applies to the column attribute storage as well.
The old attribute container was designed to store several different attributes altogether, namely,

  • hidden state,
  • filtered state,
  • automatic page break position,
  • manual page break position, and
  • whether or not a row has a manual height.

They were stored per range, not per individual row or column, so that if a range of rows had identical set of attribute values over the entire range, that attribute set would be stored as a single record. Searching for the value of an attribute for an arbitrary row was performed linearly from the first record since the core of the container itself was simply just an array.

There were primarily two problems with this storage scheme that made the container non-scalable. First, the attributes stored together in this container had different distribution patterns, which caused over-partitioning of the container and unnecessarily slowed down the queries of all stored attributes.

For instance, the hidden and filtered attributes are distributed in a very similar manner, but the manual height attribute is not necessarily distributed in a manner similar to these attributes. Because of this, storing that together with the hidden and filtered attributes unnecessarily increased the partition count, which in turn would slow down the query speed of all three attributes.

Even more problematic was the automatic page break attributes; because the automatic page breaks always need to be set for the entire sheet, increasing the row limit significantly raised the partition count. On top of that, the page breaks themselves are actually single-row attributes; it made little sense to store them in a container that was range-based.

This over-partitioning problem led to the second problem; when the container was over-partitioned, querying for an attribute value would become very slow due to the linear search algorithm used in the query, and this algorithm scales with the number of partitions. Because row attributes are used extensively in many areas of Calc’s operations, and often times in loops, the degradation of its lookup performance caused all sorts of interesting performance problems when the row limit was raised to 1 million.

New way of storing row attributes

Separation of row attributes

The first step in speeding up storage and lookup of row attributes is to separate them into own containers, to avoid the storage of one attribute affecting the storage of another. It was natural to use a range-based container to store the hidden, filtered and the manual height attributes, since these attributes typically span over many consecutive rows. The page break positions, on the other hand, should be stored as point values as opposed to range values since they rarely occur in ranges and they are always set to individual rows.

I picked STL’s std::set container to store the automatic and manual page break positions (they are stored separately in two set containers). That alone resulted in significantly speeding up the sheet pagination performance, whose performance previously suffered due to the poor storage speed of the old container. Later on I improved the pagination performance even further by modifying the pagination algorithm itself, but more on that later.

For the hidden and filtered attributes, I picked a data structure that I call the flat segment tree, which I designed and implemented specifically for this purpose. Row heights are also stored in the flat segment tree.

Flat segment tree

I named this data structure “flat segment tree” because it is a modified version of a data structure known as the segment tree, and unlike the original segment tree which supports storage of overlapping ranges, my version only stores non-overlapping ranges, hence the name “flat”. The structure of the flat segment tree largely resembles that of the original segment tree; it consists of a balanced binary tree with its leaf nodes storing the values while its non-leaf nodes storing auxiliary data used only for querying purposes. The leaf nodes are doubly-linked, allowing them a quick access to their neighboring nodes. Since ranges never overlap with each other in this data structure, one leaf node represents the end of a preceding range and the start of the range that follows. Last but not least, this data structure is a template, and allows you to specify the types of both key and value.

flat-segment-tree-lookup

There are three advantages of using this data structure: 1) compactness of storage since only the range boundaries are stored as nodes, 2) reasonably fast lookup thanks to its tree structure, and 3) a single query of a stored value also returns the lower and upper boundary positions of that range with no additional overhead. The last point is very important which I will explain later in the next section.

As an additional rule, the flat segment tree guarantees that the values of adjacent ranges are always different. There is no exception to this rule, so you can take advantage of this when you use this structure in your code.

Also, please do keep in mind that, while the lookup of a value is reasonably fast, it is not without an overhead. So, you are discouraged to perform, say, lookup for every single row when you are iterating through a series of rows in a loop. Instead, do make use of the range boundary info judiciously to skip ahead in such situation.

This data structure is distributed independently of the OOo code base, licensed under MIT/X11. You can find the source code at http://code.google.com/p/multidimalgorithm/. That project includes other data structures than the flat segment tree; however, only the flat segment tree is currently usable by 3rd party programs; the implementations of other structures are still in an experimental stage, and need to be properly templetized before becoming usable in general. Even the flat segment tree is largely undocumented. This is intentional since the API is still not entirely frozen and is subject to change in future versions. You have been warned.

Loop count reduction

Aside from the aforementioned improvement associated with the row attribute storage, I also worked on improving various algorithms used throughout Calc’s core, by taking advantage of one feature of the new data structure.
loop-for-each-row
As I mentioned earlier, the flat segment tree returns the lower and upper boundary positions of the range as part of a normal value query. You can make use of this extra piece of information to significantly reduce the number of loops in an algorithm that loops through a wide row range. Put it another way, since you already know the attribute value associated with that range, and you also know the start and end positions of that range, you don’t need to query the value for every single row position within that range, thus reducing the number of iterations in the loop. And the reduction of the loop count means the reduction of the time required to complete that operation, resulting in a better performance.

That’s the gist of the performance improvement work I did in various parts of Calc, though there were slight variations depending on which part of Calc’s code I worked on. In summary, the following areas received significant performance improvement:

  • Sheet pagination, which consisted of loops in which numerous calls are made to query row’s hidden states and row height values.
  • Print preview, mostly due to the improvement of the pagination performance.
  • Calculation of drawing object’s vertical position

I’m sure there are other areas where the performance still needs improvement. As this is an on-going effort, we will work on resolving any other outstanding issues as we discover them.

Other related work

In addition to the re-work of the row attribute storage and the performance improvement involving the row attribute queries, I’ve also made other changes to improve performance and ensure that Calc’s basic usability is not sacrificed.

Removal of redundant pagination

Prior to my row limit increase work, Calc would re-calculate page break positions again and again even when no changes were made to the document that would alter page break positions, such as changing row heights, filtering rows, inserting manual page breaks, and so on. Because the pagination operation became much more expensive after the row limit increase, I have decided to remove this redundancy so that the re-pagination is done only when necessary. This change especially made huge impact in print preview performance, since (for whatever reason) Calc was performing full pagination every time you move the mouse cursor within the preview pane, even when the movement was only by one pixel! Removal of such redundant re-pagination has brought sanity back to the print preview experience.

Efficient zoom level calculation

The row limit increase also caused the performance degradation of calculating the correct zoom size to fit the document within specified page size. Calc does this when you specify your document to “fit within n pages wide and y pages tall” or “fit to n pages in total”. The root cause was again in the degraded performance in pagination. This time, however, I could not use the trick of “performing pagination only once”, because we do need to perform full pagination continuously at different zoom levels in order to find a correct zoom level.

The solution I employed was to reduce the number of re-pagination by using the bisection method to arrive at the correct zoom level. The old code worked like this:

  1. Initialize the zoom level to 100%, and perform full pagination.
  2. If that doesn’t fit the required page size, decrement the zoom level by 1%, and perform full pagination once again.
  3. If that doesn’t fit, decrement the zoom level by 1%, and try again.
  4. Continue this until the correct zoom level is reached.

Of course, if the correct zoom level is far below the initial value of 100%, this algorithm is not very efficient. If the desired zoom level is 35%, for example, Calc would need to perform full pagination 66 times. Switching to the bisection method here reduced the full pagination count roughly down to the neighborhood of 5 or 6. At the time I worked on this, each full pagination took about 1 second. So the reduction of pagination count from 66 to 5 roughly translated to the reduction of the zoom level calculation from 1 minute to 5 seconds. Suffice it to say that this made a big difference.

Even better news is that the performance of this operation is much faster today, thanks to the improvement I made in the pagination performance in general.

Calculation of autofill marker position

autofill
When making a selection, Calc puts the little square at the lower-right corner of the selection. That’s called an autofill marker, and it’s there to let you drag selection to fill values.

Interestingly, calculating its position (especially its vertical position) turned out to be a very slow operation when the marker was positioned close to the bottom of the sheet. Worse is the fact that Calc calculated its position even when it was outside the visible area. The slowdown caused by this was apparent especially when making column selection. Because selecting columns always places the autofill marker at the last row of the sheet, increasing the row limit made that process sluggish. The solution was to simply detect whether the autofill marker is outside the visible area, and if it is, skip calculating its position (since there is no point calculating its position if we don’t need to display it). That made the process of column selection back to normal again.

However, the sluggishness of making selection can still manifest itself under the right (wrong?) condition even with this change. We still need to speed up the calculation of its vertical position, by improving the calculation algorithm itself.

Show stoppers for the upstream build

I sat down and briefly discussed with Niklas Nebel and Eike Rathke, Sun’s Calc co-leads, when we met during last year’s OOoCon in Orvieto, about the possibility of increasing the row limit in the upstream version of Calc. During our discussion, I was told that, in addition to the general performance issues most of which I’ve already resolved, we will need to resolve at least two more outstanding issues before they can set the row limit to 1 million in the upstream build.

First, we need to improve the performance of the formula calculation and the value change propagation mechanism (that we call “broadcasting”). The existing implementation is still tuned for the grid size of 65536 rows; we need to re-tune that for 1 million rows and to ensure that the performance will not suffer after the row limit increase.

cell-note-misplaced

Second, we need to resolve the incorrect positioning of drawing objects at higher row positions. This one is somewhat tricky, since the drawing objects are drawn entirely independent of the sheet grid, and the coerce resolution of the drawing layer causes the vertical position of a drawing object to deviate from its intended position. Generally speaking, the higher the row position the more deviation results. With the maximum of 65536 rows, however, it was not such a big issue since the amount of deviation was barely noticeable even at the highest row position. But because the problem becomes much more noticeable with 1 million rows, this needs to be addressed somehow.

Going forward…

Going forward, I will continue to hunt for the remaining performance issues, and squash them one by one. The major ones should all be resolved by now, so what’s remaining should be some corner case issues, performance-wise. As for the two outstanding issues I mentioned in the previous section, we will have to take a good look at them at some point. Whether or not they are really show stoppers is somewhat subject to personal view point, but they are real issues needing resolution, for sure, no matter what their perceived severity is.

Also, as of this writing, the manual row size attribute is still stored in the old, array-based container. It will probably make sense to migrate that to the flat segment tree, so that we can eliminate the old container once and for all, and have a fresh start with the new container. Having said that, doing so would require another round of refactoring of non-trivial scale, it should be conducted with care and proper testing.

The ODS export filter still needs re-work. Currently, all row attributes which are now stored separately, are temporarily merged back into the old array-based container before exporting the document to ODS. The reason is that the ODS export filter code still expects the partitioning behavior of the old container during the export of row styles. In order to fully embrace the new storage of row attributes, that code needs to be adjusted to work with the new storage scheme. Again, this will require a non-trivial amount of code change, thus should be conducted with care.

Calculation of vertical position of various objects, such as the autofill marker can still use some algorithmic improvement. We can make them more efficient by taking advantage of the flat segment tree in a way similar to how the pagination algorithm was made more efficient.

Conclusion

This concludes my write-up on the current status of Calc’s row limit increase work. I hope I’ve made it clear that work is underway toward making that happen without degrading Calc’s basic usability. As a matter of fact, the row limit has already been increased to 1 million in some variants of OOo, such as Go-OO. I believe we’ll be able to increase the row limit in the upstream version in the not-so-distant future as long as we keep working at the remaining issues.

That’s all I have to say for now. Thank you very much, ladies and gentlemen.

Posted on

Excel sheet protection password hash

Share Button

When you protect either your workbook or one of your worksheets with a password in Excel, Excel internally generates a 16-bit hash of your password and stores it instead of the original password text. The hashing algorithm used for that was previously unknown, but thanks to the infamous Office Open XML specification it is now documented for the world to see (take a look at Part 4, Section 3.3.1.81 – Sheet Protection Options for the details). Thankfully, the algorithm is identical for all recent versions of Excel including XP, 2003 and 2007, so you can simply reuse the documented algorithm for the older versions of Excel too.

But alas! the documented algorithm is incorrect; it does not produce correct hash values. Being determined to find out the correct algorithm, however, I started to analyze the hashes that the documented algorithm produces, and compare them with the real hash values that Excel generates, in order to decipher the correct algorithm.

In the end, the documented algorithm was, although not accurate, pretty close enough that I was able to make a few changes and derive the algorithm that generates correct values. The following code:

#include <stdio.h>
 
using namespace std;
 
typedef unsigned char sal_uInt8;
typedef unsigned short sal_uInt16;
 
sal_uInt16 getPasswordHash(const char* szPassword)
{
    sal_uInt16 cchPassword = strlen(szPassword);
    sal_uInt16 wPasswordHash = 0;
    if (!cchPassword)
        return wPasswordHash;
 
    const char* pch = &szPassword[cchPassword];
    while (pch-- != szPassword)
    {
        wPasswordHash = ((wPasswordHash >> 14) & 0x01) | 
                        ((wPasswordHash << 1) & 0x7fff);
        wPasswordHash ^= *pch;
    }
 
    wPasswordHash = ((wPasswordHash >> 14) & 0x01) | 
                    ((wPasswordHash << 1) & 0x7fff);
 
    wPasswordHash ^= (0x8000 | ('N' << 8) | 'K');
    wPasswordHash ^= cchPassword;
 
    return wPasswordHash;
}
 
int main (int argc, char** argv)
{
    if (argc < 2)
        exit(1);
 
    printf("input password = %s\n", argv[1]);
    sal_uInt16 hash = getPasswordHash(argv[1]);
    printf("hash = %4.4X\n", hash);
 
    return 0;
}

produces the right hash value from an arbitrary password. One caveat: this algorithm takes an 8-bit char array, so if the input value consists of 16-bit unicode characters, it needs to be first converted into 8-bit character array. The conversion algorithm is also documented in the OOXML specification. I have not tested it yet, but I hope that algorithm is correct. ;-)

Posted on

Sudoku Solver

Share Button

I don’t know about the rest of the world, but the part of the world I live in, Sudoku was spreading like a wildfire. It was almost to the point that you couldn’t be in a place where you didn’t see anyone playing Sudoku in one form or another. This trend seems to have died down a bit, but Sudoku still is quite popular puzzle and a good way to spend (waste?) some time exercising your brain cells.

I, on the other hand, have never played Sudoku. But that doesn’t mean that I can’t write a solver for it. It’s written in Python, and is pretty simple and straightforward. It uses a recursive backtracking to find a solution, so there is no fancy algorithm there. Still, it manages to solve most of the Sudoku puzzles I’ve encountered within a second. For some harder ones it spends about a few seconds, but it’s still within what I consider a reasonable time frame.

How to use it is pretty simple. When you download and unpack the file, you should see a file named sdksolve in the base directory. It takes a text file containing a Sudoku grid as an input file, and spits out the solution to standard output. There are some example input files under the example directory, so you can use those to see how it works. Here is an example run:

./sdksolve sample/web1.txt
Sudoku Solver by Kohei Yoshida
--------------------------------------------------------------------
Input Sudoku Grid
--------------------------------------------------------------------
5 * * 3 * * 1 * *
7 4 * 2 * * * 3 6
* * * * 1 * * 2 4
* * * 7 2 * 8 6 *
4 * 2 * * * 7 * 5
* 7 9 * 8 1 * * *
2 1 * * 7 * * * *
3 6 * * * 2 * 5 8
* * 4 * * 6 * * 1
--------------------------------------------------------------------
5 2 6 3 4 9 1 8 7
7 4 1 2 5 8 9 3 6
8 9 3 6 1 7 5 2 4
1 3 5 7 2 4 8 6 9
4 8 2 9 6 3 7 1 5
6 7 9 5 8 1 3 4 2
2 1 8 4 7 5 6 9 3
3 6 7 1 9 2 4 5 8
9 5 4 8 3 6 2 7 1
valid sudoku grid!
number of iterations: 116

So, here goes yet-another-Sudoku-solver out in the wild. Have fun! :-)

Posted on

New LU factorization in matrix inverse algorithm

Share Button

One of the things I wanted to do as a remedy to my simplex algorithm (refer to my last blog entry) was to switch to another algorithm for LU factorization which is used in my matrix inverse algorithm. The original LU factorization algorithm obviously was not robust enough to inverse an initial matrix generated in solving Markus’ model. This time, instead of blindly looking for a new algorithm to use all over the net, I decided to dive into Calc’s code to see what algorithm Calc uses internally for matrix inversion since Calc was able to inverse the very matrix my own algorithm was not.

Of course, I can’t just copy and paste Calc’s matrix inverse code, but luckily there was a reference within the code from which it was derived, and I just happened to have a copy of that very same reference which one of my friends was kind enough to lend to me a few weeks ago. Lucky me!

Anyway, now my solver can at least solves Markus’ model, though my solution differs from the Excel Solver’s solution that he included because of simplex’s positive variable limitation (his Excel solution included negative numbers). Adding support for negative numbers shouldn’t be too complex, but requires a bit more work.

The new snapshot (revision 101) is up which includes this new LU factorization algorithm.

Posted on

Studying…

Share Button

I have been busy studying data structure for the past week to partly refresh and partly deepen my understanding of the subject. The obvious side-effect of this is that I haven’t been able to spend much time coding. But hopefully this study effort will pay off.

Also, I’m firmly convinced that I need to spend significant amount of time studying on matrix computation essentials in order to be able to develop reasonably-fast matrix calculation algorithms (I got the book by the way). The algorithms I use for linear programming relies heavily on matrix operations, so this effort is absolutely important. And yes, I am aware that there are libraries out there that already do fast matrix computations, but using them without having some idea of what they may be doing internally bothers me quite a bit.

Meanwhile, my patch for fixing Calc’s erf/erfc functions (i55735) is proposed for 2.0.2. Jody helped me on minor performance improvement.