In this post, I’m going to share the results of some benchmark testing I have done on multi_type_vector, which is included in the mdds library. The benchmark was done to measure the impact of the change I made recently to improve the performance on block searches, which will affect a major part of its functionality.
Background
One of the data structures included in mdds, called multi_type_vector, stores values of different types in a single logical vector. LibreOffice Calc is one primary user of this. Calc uses this structure as its cell value store, and each instance of this value store represents a single column instance.
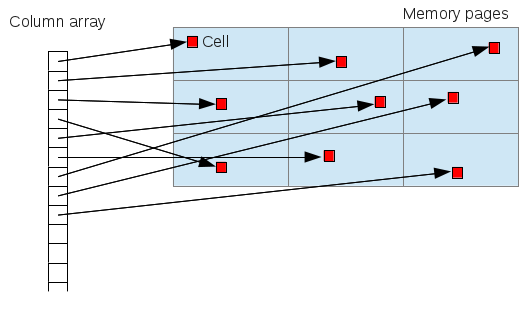
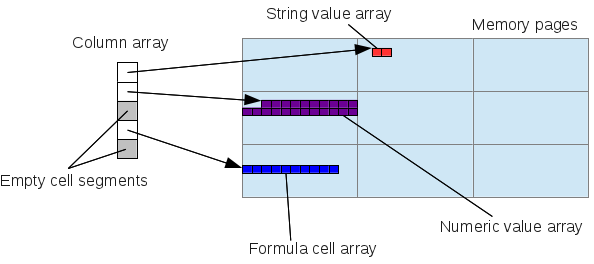
Internally, multi_type_vector creates multiple element blocks which are in turn stored in its parent array (primary array) as block structures. This primary array maps a logical position of a value to the actual block structure that stores it. Up to version 1.5.0, this mapping process involved a linear search that always starts from the first block of the primary array. This was because each block structure, though it stores the size of the element block, does not store its logical position. So the only way to find the right element block that intersects the logical position of a value is to scan from the first block and keep accumulating the sizes of the encountered blocks. The following diagram depicts the structure of multi_type_vector’s internal store as of 1.5.0:
The reason for not storing the logical positions of the blocks was to avoid having to update them after shifting the blocks after value insertion, which is quite common when editing spreadsheet documents.
Of course, sometimes one has to perform repeated searches to access a number of element values across a number of element blocks, in which case, always starting the search from the first block, or block 0, in every single search can be prohibitively expensive, especially when the vector is heavily fragmented.
To alleviate this, multi_type_vector provides the concept of position hints, which allows the caller to start the search from block N where N > 0. Most of multi_type_vector’s methods return a position hint which can be used for the next search operation. A position hint object stores the last position of the block that was either accessed or modified by the call. This allows the caller to chain all necessary search operations in such a way to scan the primary array no more than once for the entire sequence of search operations. It was largely inspired by std::map’s insert method which provides a very similar mechanism. The only prerequisite is that access to the elements occur in perfect ascending order. For the most part, this approach worked quite well.
The downside of this is that there are times you need to access multiple element positions and you cannot always arrange your access pattern to take advantage of the position hints. This is the case especially during multi-threaded formula cell execution routine, which Calc introduced some versions ago. This has motivated us to switch to an alternative lookup algorithm, and binary search was the obvious replacement.
Binary search
Binary search is an algorithm well suited to find a target value in an array where the values are stored in sorted order. Compared to linear search, binary search performs much faster except for very small arrays. People often confuse this with binary search tree, but binary search as an algorithm does not limit its applicability to just tree structure; it can be used on arrays as well, as long as the stored values are sorted.
While it’s not very hard to implement binary search manually, the C++ standard library already provides several binary search implementations such as std::lower_bound and std::upper_bound.
Switch from linear search to binary search
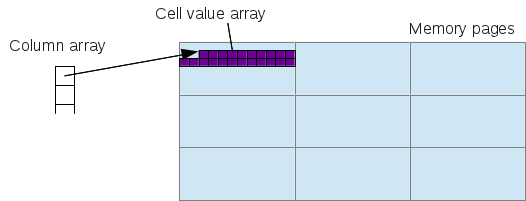
The challenge for switching from linear search to binary search was to refactor multi_type_vector’s implementation to store the logical positions of the element blocks and update them real-time, as the vector gets modified. The good news is that, as of this writing, all necessary changes have been done, and the current master branch fully implements binary-search-based block position lookup in all of its operations.
Benchmarks
To get a better idea on how this change will affect the performance profile of multi_type_vector, I ran some benchmarks, using both mdds version 1.5.0 – the latest stable release that still uses linear search, and mdds version 1.5.99 – the current development branch which will eventually become the stable 1.6.0 release. The benchmark tested the following three scenarios:
-
set()that modifies the block layout of the primary array. This test sets a new value to an empty vector at positions that monotonically increase by 2, until it reaches the end of the vector. -
set()that updates the value of the last logical element of the vector. The update happens without modifying the block layout of the primary array. Like the first test, this one also measures the performance of the block position lookup, but since the block count does not change, it is expected that the block position lookup comprises the bulk of its operation. -
insert()that inserts a new element block at the logical mid-point of the vector and shifts all the elements that occur below the point of insertion. The primary array of the vector is made to be already heavily fragmented prior to the insertion. This test involves both block position lookup as well as shifting of the element blocks. Since the new multi_type_vector implementation will update the positions of element blocks whose logical positions have changed, this test is designed to measure the cost of this extra operation that was previously not performed as in 1.5.0.
In each of these scenarios, the code executed the target method N number of times where N was specified to be 10,000, 50,000, or 100,000. Each test was run twice, once with position hints and once without them. Each individual run was then repeated five times and the average duration was computed. In this post, I will only include the results for N = 100,000 in the interest of space.
All binaries used in this benchmark were built with a release configuration i.e. on Linux, gcc with -O3 -DNDEBUG flags was used to build the binaries, and on Windows, MSVC (Visual Studio 2017) with /MD /O2 /Ob2 /DNDEBUG flags was used.
All of the source code used in this benchmark is available in the mdds perf-test repository hosted on GitLab.
The benchmarks were performed on machines running either Linux (Ubuntu LTS 1804) or Windows with a variety of CPU’s with varying number of native threads. The following table summarizes all test environments used in this benchmark:
It is very important to note that, because of the disparity in OS environments, compilers and compiler flags, one should NOT compare the absolute values of the timing data to draw any conclusions about CPU’s relative performance with each other.
Results
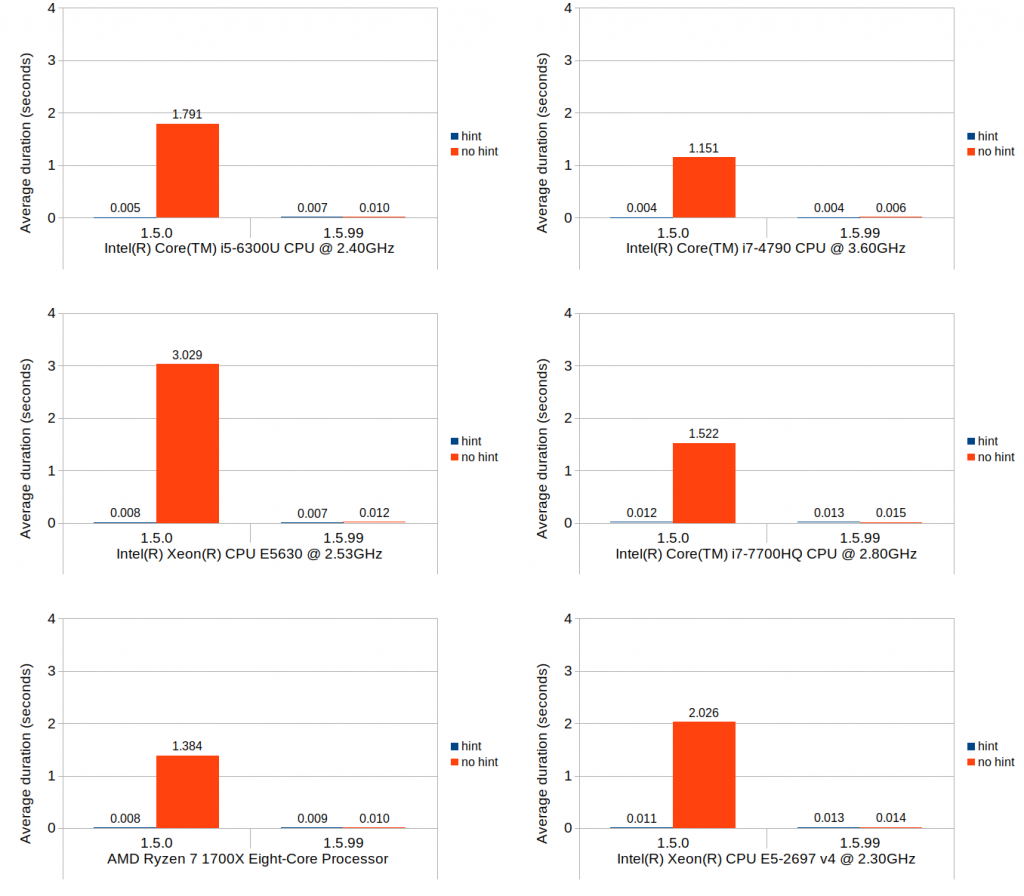
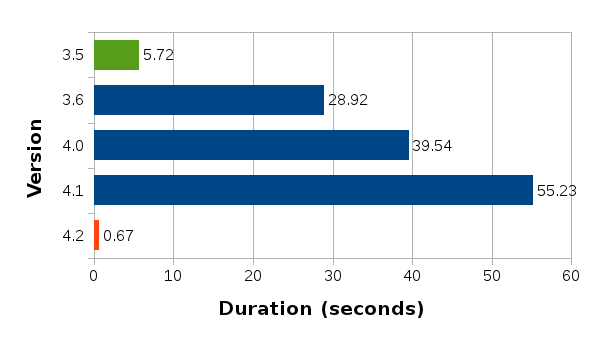
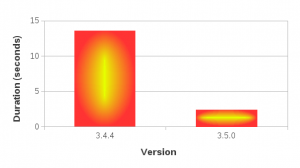
Scenario 1: set value at monotonically increasing positions
This scenario tests a set of operations that consists of first seeking the position of a block that intersects with the logical position, then setting a new value to that block which causes that block to split and a new value block inserted at the point of split. The test repeats this process 100,000 times, and in each iteration the block search distance progressively increases as the total number of blocks increases. In Calc’s context, scenarios like this are very common especially during file load.
Without further ado, here are the results:
You can easily see that the binary search (1.5.99) achieves nearly the same performance as the linear search with position hints in 1.5.0. Although not very visible in these figures due to the scale of the y-axes, position hints are still beneficial and do provide small but consistent timing reduction in 1.5.99.
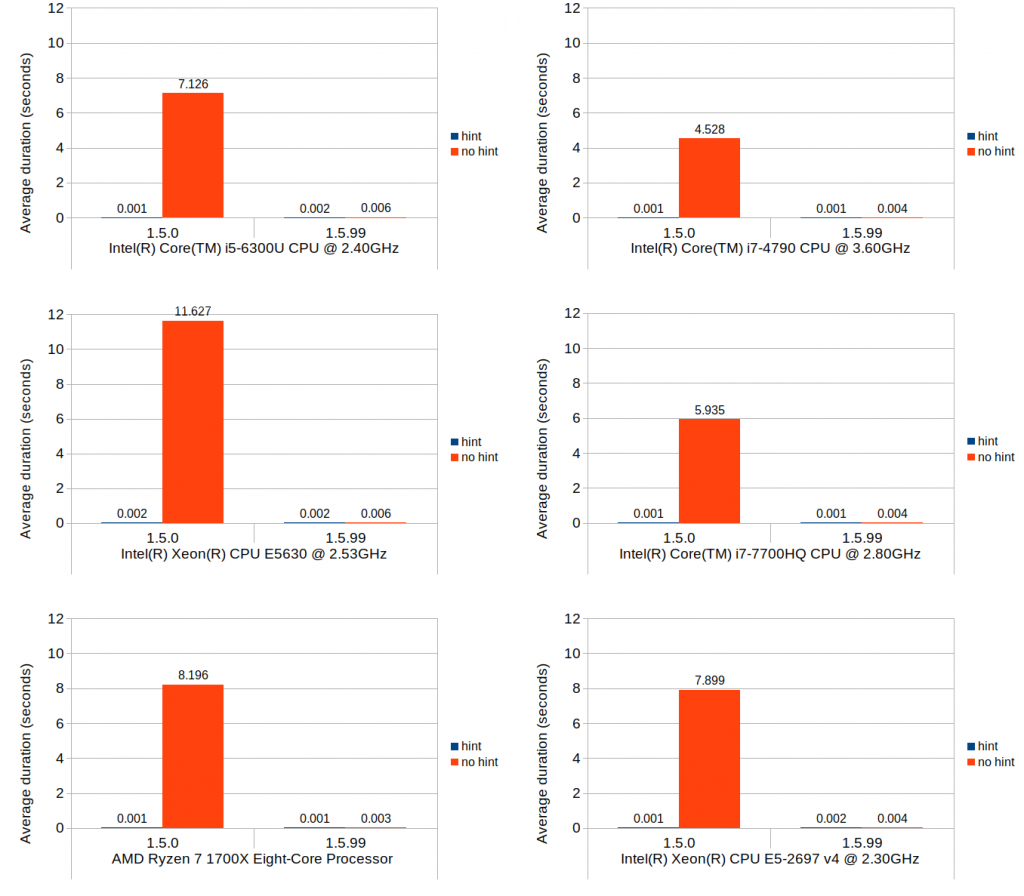
Scenario 2: set at last position
The nature of what this scenario tests is very similar to that of the previous scenario, but the cost of the block position lookup is much more emphasized while the cost of the block creation is eliminated. Although the average durations in 1.5.0 without position hints are consistently higher than their equivalent values from the previous scenario across all environments, the overall trends do remain similar.
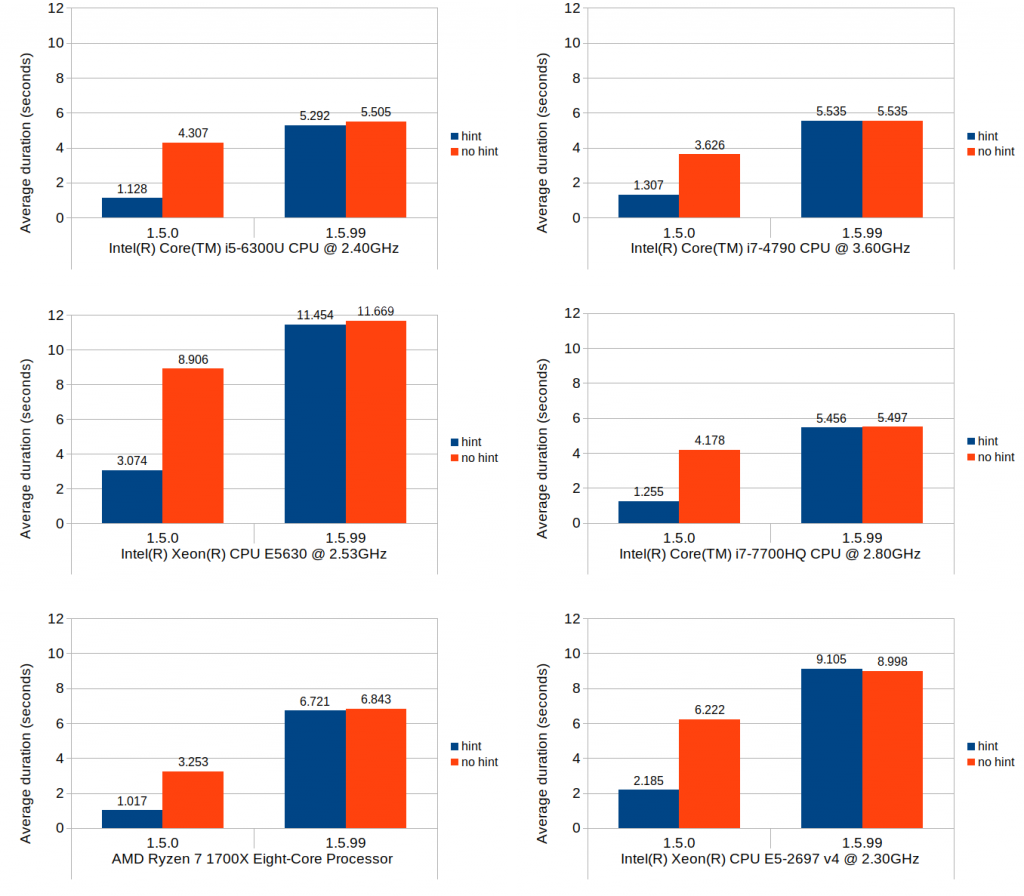
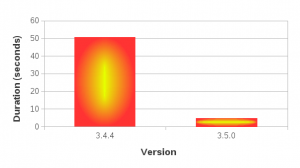
Scenario 3: insert and shift
This last scenario was included primarily to test the cost of updating the stored block positions after the blocks get shifted, as well as to quantify how much increase this overhead would cause relative to 1.5.0. In terms of Calc use case, this operation roughly corresponds with inserting new rows and shifting of existing non-empty rows downward after the insertion.
Without further ado, here are the results:
These results do indicate that, when compared to the average performance of 1.5.0 with position hints, the same operation can be 4 to 6 times more expensive in 1.5.99. Without position hints, the new implementation is more expensive to a much lesser degree. Since the scenario tested herein is largely bottlenecked by the block position updates, use of position hints seems to only provide marginal benefit.
Adding parallelism
Faced with this dilemma of increased overhead, I did some research to see if there is a way to reduce the overhead. The suspect code in question is in fact a very simple loop, and all its does is to add a constant value to a known number of blocks:
template void multi_type_vector<_CellBlockFunc, _EventFunc>::adjust_block_positions(size_type block_index, size_type delta) { size_type n = m_blocks.size(); if (block_index >= n) return; for (; block_index < n; ++block_index) m_blocks[block_index].m_position += delta; } |
Since the individual block positions can be updated entirely independent of each other, I decided it would be worthwhile to experiment with the following two types of parallelization techniques. One is loop unrolling, the other is OpenMP. I found these two techniques attractive for this particular case, for they both require very minimal code change.
Adding support for OpenMP was rather easy, since all one has to do is to add a #pragma line immediately above the loop you intend to parallelize, and add an appropriate OpenMP flag to the compiler when building the code.
Adding support for loop unrolling took a little fiddling around, but eventually I was able to make the necessary change without breaking any existing unit test cases. After some quick experimentation, I settled with updating 8 elements per iteration.
After these changes were done, the above original code turned into this:
template void multi_type_vector<_CellBlockFunc, _EventFunc>::adjust_block_positions(int64_t start_block_index, size_type delta) { int64_t n = m_blocks.size(); if (start_block_index >= n) return; #ifdef MDDS_LOOP_UNROLLING // Ensure that the section length is divisible by 8. int64_t len = n - start_block_index; int64_t rem = len % 8; len -= rem; len += start_block_index; #pragma omp parallel for for (int64_t i = start_block_index; i < len; i += 8) { m_blocks[i].m_position += delta; m_blocks[i+1].m_position += delta; m_blocks[i+2].m_position += delta; m_blocks[i+3].m_position += delta; m_blocks[i+4].m_position += delta; m_blocks[i+5].m_position += delta; m_blocks[i+6].m_position += delta; m_blocks[i+7].m_position += delta; } rem += len; for (int64_t i = len; i < rem; ++i) m_blocks[i].m_position += delta; #else #pragma omp parallel for for (int64_t i = start_block_index; i < n; ++i) m_blocks[i].m_position += delta; #endif } |
I have made the loop-unrolling variant of this method a compile-time option and kept the original method intact to allow on-going comparison. The OpenMP part didn’t need any special pre-processing since it can be turned on and off via compiler flag with no impact to the code itself. I needed to switch the loop counter from the original size_type (which is a typedef to size_t) to int64_t so that the code can be built with OpenMP enabled on Windows, using MSVC. Apparently the Microsoft Visual C++ compiler requires the loop counter to be a signed integer for the code to even build with OpenMP enabled.
With these changes in, I wrote a separate test code just to benchmark the insert-and-shift scenario with all permutations of loop-unrolling and OpenMP. The number of threads to use for OpenMP was not specified during the test, which would cause OpenMP to automatically use all available native threads.
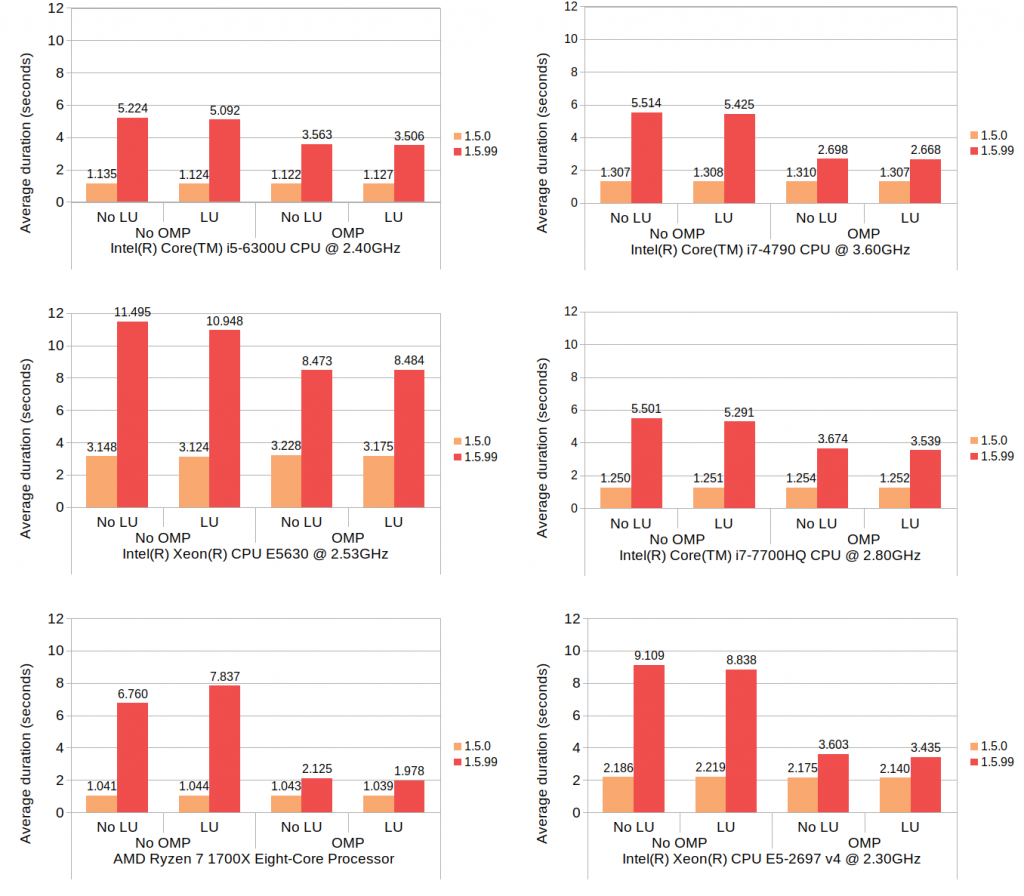
With all of this out of the way, let’s look at the results:
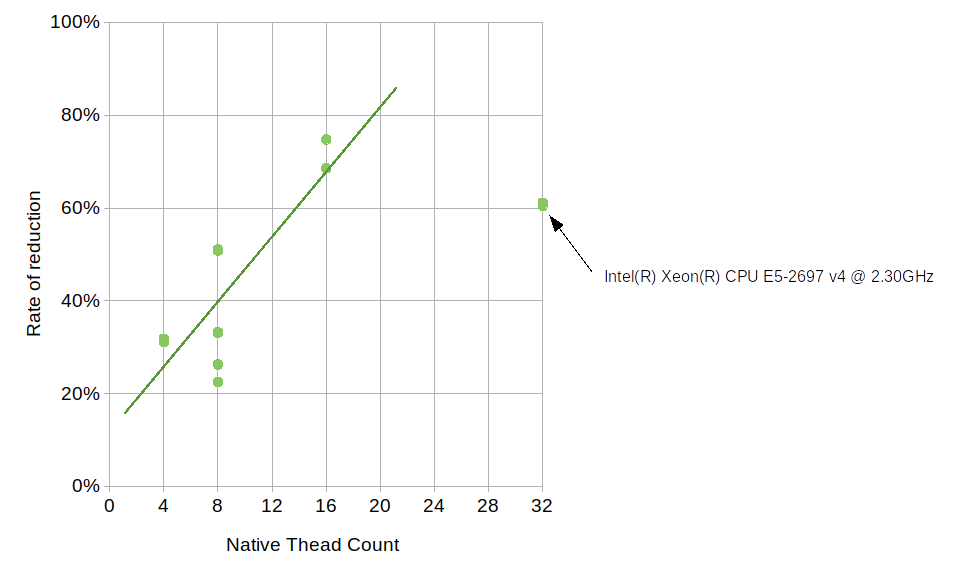
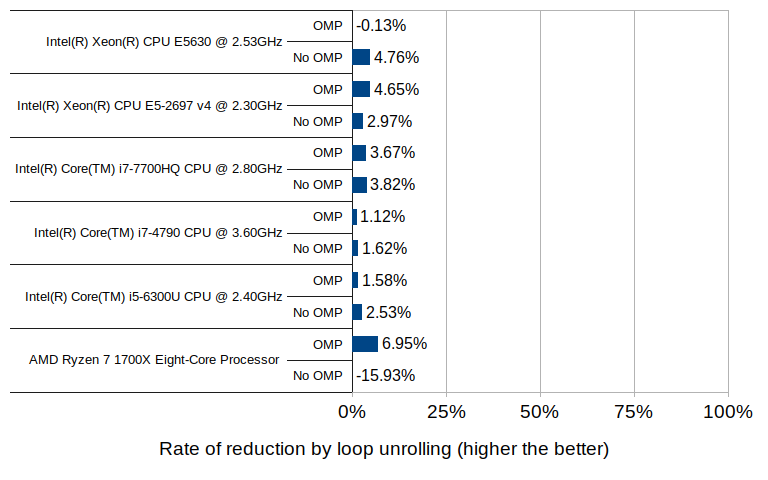
Here, LU and OMP stand for loop unrolling and OpenMP, respectively. The results from each machine consist of four groups each having two timing values, one with 1.5.0 and one with 1.5.99. Since 1.5.0 does not use neither loop unrolling nor OpenMP, its results show no variance between the groups, which is expected. The numbers for 1.5.99 are generally much higher than those of 1.5.0, but the use of OpenMP brings the numbers down considerably. Although how much OpenMP reduced the average duration varies from machine to machine, the number of available native threads likely plays some role. The reduction by OpenMP on Core i5 6300U (which comes with 4 native threads) is approximately 30%, the number on Ryzen 7 1700X (with 16 native threads) is about 70%, and the number on Core i7 4790 (with 8 native threads) is about 50%. The relationship between the native thread count and the rate of reduction somewhat follows a linear trend, though the numbers on Xeon E5-2697 v4, which comes with 32 native threads, deviate from this trend.
The effect of loop unrolling, on the other hand, is visible only to a much lesser degree; in all but two cases it has resulted in a reduction of 1 to 7 percent. The only exceptions are the Ryzen 7 without OpenMP which denoted an increase of nearly 16%, and the Xeon E5630 with OpenMP which denoted a slight increase of 0.1%.
The 16% increase with the Ryzen 7 environment may well be an outlier, since the other test in the same environment (with OpenMP enabled) did result in a reduction of 7% – the highest of all tested groups.
Interpreting the results
Hopefully the results presented in this post are interesting and provide insight into the nature of the change in multi_type_vector in the upcoming 1.6.0 release. But what does this all mean, especially in the context of LibreOffice Calc? These are my personal thoughts.
- From my own observation of having seen numerous bug reports and/or performance issues from various users of Calc, I can confidently say that the vast majority of cases involve reading and updating cell values without shifting of cells, either during file load, or during executions of features that involve massive amounts of cell I/O’s. Since those cases are primarily bottlenecked by block position search, the new implementation will bring a massive win especially in places where use of position hints was not practical. That being said, the performance of block search will likely see no noticeable improvements even after switching to the new implementation when the code already uses position hints with the old implementation.
- While the increased overhead in block shifting, which is associated with insertion or deletion of rows in Calc, is a certainly a concern, it may not be a huge issue in day-to-day usage of Calc. It is worth pointing out that that what the benchmark measures is repeated insertions and shifting of highly fragmented blocks, which translates to repeated insertions or deletions of rows in Calc document where the column values consist of uniformly altering types. In normal Calc usage, it is more likely that the user would insert or delete rows as one discrete operation, rather than a series of thousands of repeated row insertions or deletions. I am highly optimistic that Calc can absorb this extra overhead without its users noticing.
- Even if Calc encounters a very unlikely situation where this increased overhead becomes visible at the UI level, enabling OpenMP, assuming that’s practical, would help lessen the impact of this overhead. The benefit of OpenMP becomes more elevated as the number of native CPU threads becomes higher.
What’s next?
I may invest some time looking into potential use of GPU offloading to see if that would further speed up the block position update operations. The benefit of loop unrolling was not as great as I had hoped, but this may be highly CPU and compiler dependent. I will likely continue to dig deeper into this and keep on experimenting.